Gravitational potential due to a spherical shell

Gravitational potential due to a spherical shell:

1) At a point outside the shell:

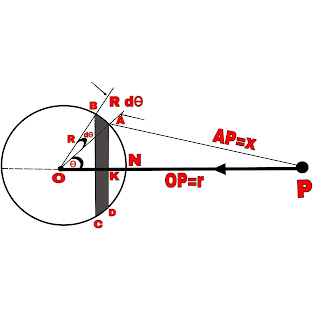
Consider a uniform spherical shell of radius R.

Let P be a point outside the spherical shell at a distance ‘r ' from the centre O of the shell.

Let ϱ = Mass per unit area of the surface.

As shown in figure, two planes AD and BC cut the shell vertically.

The element between the two planes is a slice ABCD in the form of a ring  of small angular width dϴ with the OP as axis.

Each element of the ring is at a distance , AP = x from the outside point P.

.•. Thickness of the shell, AB = R dϴ 

Radius of the shell, CK = R sinϴ

.•. Surface area of the slice= (2πR sinϴ) (R dϴ )  = 2πR² sinϴ dϴ 

.•. Mass of the slice= Surface area of  slice× Mass per unit area (ϱ)

Figure: Gravitational potential at a point outside the spherical shell.

.•. Mass of the slice, Mring = 2πR²sinϴ dϴ ϱ

.•. potential at P due to the ring is :

dV = - GMring
                X

      =   - G(2πR²ϱsinϴ dϴ )/x    .....(1)

      In ∆ APO :    x² = r² + R² - 2rR cosϴ

Differentiating above equation, we get :

      2x dx = 2rR sinϴ dϴ      
                           ( since,R and r are constant ) 

      .•. x = rR sinϴ dϴ 
                     dx

Substituting this value of ‘x' in eq. (1) , we get :

dV = - G ( 2πR²ϱsinϴ dϴ ) dx 
                     rR sinϴ dϴ

     

     = - 2πRϱG dx

              r

Integrating above equation for the whole shell between the limits, 

x = ( r- R ) to x = ( r+R ) , we get :

But, 4πR²ϱ = M   ( Mass of the whole shell )

.•.  V = - GM 
                 r     ...... (2)

Thus, for a point outside the shell, the shell behabes as if the whole mass is concentrated at the centre of the shell.

Now, the intensity of gravitational field at a point outside the shell is given by:

E = - dV / dr  

  

   = - d / dr ( - GM / r )

.•. E = - GM / r²      ...... (3)

Negative sign shows that intensity of gravitational field is directed towards the centre O of the shell.

(2) Potential on the surface of the shell :

For a point on the surface of the shell, r= R.

.•. Potential ,  V = - GM / R

Intensity of the field,  E = - GM / R²