Equivalent focal length of coaxial lens system

Equivalent focal length of coaxial lens system:

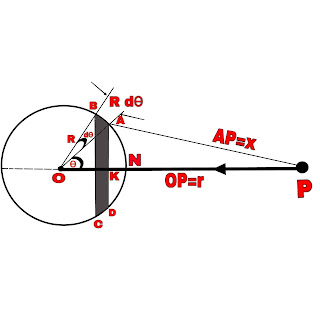
Consider two thin lenses L₁ and L₂ focal length f₁ and f₂ respectively. These are placed in air separated by a distance ‘a'. Let a light ray AB is incident on lens L₁, parallel to the principal axis at a height X above the axis. After refraction of this ray through lens L₁, it deviates through an angle δ₁ and the emergent ray ( in the absence of L₂ ), passes through second principal focus of L₁,
Which is at D. The ray AB is deviated through an angle δ₁ by the lens L₁. In figure A.

Let, O₁B = x ,      O₁O₂  = a,      O₂ C = y

F₁ and F₂  are focal points of the optical system.
P₁ and P₂  are principal points of the optical system.
δ₁  = tan δ₁  = O₁B  = X
                         O₁D    f₁

.•. Derivation produced by first lens = δ₁= x
                                                                            f₁

The emergent ray from the lens L₁ meets the lens L₂ at C which is at a  height y above the axis. After refraction through lens L₂ the emergent ray meets the axis at F₂ which is second focal point of the lens system. The lens L₂deviated the ray BC further through  δ₂.

Geometrical Optics and Interference

.•. Deviation produced by the second lens
     = δ₂ = y / f₂

When AB , the incident ray and CF₂, the emergent ray are produced, they  meet at E. Then a single convex lens placed at EP₂ having focal length P₂F₂ ( = f ) is equivalent focal length of the lens system.

.•. Deviation produced by equivalent lens
    = δ = EP₂  /  P₂F₂

  δ = x / f

Deviation produced by equivalent lens system is  the algebraic sum of deviation produced by individual lens.

.•. δ = δ₁+ δ₂

.•. x = x +  y 
    f     f₁    f₂      ......( 1 )

From figure A.
           
            y = HO₂ - HC
               = x - a. δ₁
                                 {since angle = arc / radius
                                   δ₁ =  HC/ BH = HC / a }
               = x - a. x /f₁

           y  = x (1- a/f₁ )    .....( 2 )

   Putting this value of y in equation (1)

    x = x +  y (1- a  )
    f     f₁    f₂       f₁

     1= 1 +  1 (1- a  )
    f     f₁    f₂       f₁

    1= 1 +  1  -     a        ..... (3)
    f     f₁    f₂      f₁f₂


Where f is the equivalent focal length of coaxial lens system.

a) power of lens :

Power of a lens is its ability to converge or diverge the rays incident on it. The power of lens is the reciprocal of its focal length in meters.

 Power of lens =              1                          
                              Focal length in meters

The unit of power of lens is diopter.

A convex lens of small focal length produces a large converging effect while a convex lens of large focal length produces a small converging effect. So power of a convex lens is taken as positive. A concave lens produces divergence. Therefore, power of cancave lens produces divergence. Therefore , power of concave lens is taken as negative.

b) power of coaxial lens system:

When two thin lenses of focal lengths  f₁ and f₂ are placed coaxially and separated by a distance "a" , then equivalent focal length f of lens system is given by



    1= 1 +  1  -     a     
    f     f₁    f₂      f₁f₂

But, power =                  1                           
                         Focal length( in meters )

.•. P = P₁ + P₂ - aP₁P₂

.•. where P is the equivalent power of coaxial lens system.

c) Position of cardinal point :

(i) Second principal point

Let  β = O₂P₂ = Distance of the second principal point from the second lens.

And ɑ = Distance of the first principal point from the first lens.

The calculate the value of β we have to produced as follows: from figure .A.

O₂P₂ = P₂F₂ - O₂F₂ = f - O₂F₂   .....(4)

Now , the triangles, ∆EP₂F₂ and ∆CO₂F₂ are similar Geometrical Optics and IntererencIn

.•. EP₂ = P₂F₂   i.e   x =     f .  
    CO₂    O₂F₂          y     O₂F₂

  O₂F₂ = y. f
              x

.•. putting the value of ‘y' from equation (2) we get ,


  O₂F₂  = x (1- a  )f = ( 1- a  )f
                        f₁               f₁
                        x

putting the value of  O₂F₂  in equation ..(4) we get,

 O₂F₂ = f - (1-a  )f = a . f
                      f₁        f₁

Since P₂ lies on the left side of lens L₂.

•.• O₂F₂ = - β
     
.•.          β  = - a. f 
                         f₁        .....(5)

So second principal point ( plane ) P₂ is at a distance "β " to the left from the second lens.

ii) First principal point :  To calculate the value of ɑ we have to consider rays parallel to principal axis from the right hand side as shown in figure B.

Proceedings in the similar manner as described above we get,

 O₁P₁ = ɑ = a.f
                      f₂       .....(6)

So, first principal point P₁ is at a distance "ɑ" to the right from the first lens.

Now, as  the medium on the two side of the lens system is same, the nodal points N₁ and N₂ coincide with P₁ and P₂.

iii ) Second focal point : The distance of the second focal point F₂ from the second lens L₂ will be O₂F₂ and is given by.

O₂F₂ = P₂F₂ - P₂O₂
         = f - (- O₂P₂ )
         = f + O₂P₂
         = f + β
         = f + (- af )
                      f₁
         = f + ( 1- af )
                         f₁

iv) First focal point : The distance of the first focal point F₁ from the first lens L₁ will be O₁F₁ and is given by

       O₁F₁ = P₁F₁ - P₁O₁
                = -f - (-O₁P₁ )
                = -f + O₁P₁
                = -f + ɑ
                = - f + af
                            f₂
                = - f ( 1- a)
                              f₂

Geometrical Optics and Interference

Let O = Positive of object
        I = Positive of image
       P₁ = First principal point
       P₂ = Second principal point
       u = O₁O= Object distance from the first lens.
        v =O₂I= Image distance from the second lens.
        U= P₁O= Object distance from the first principal point.
        V= P₂I= Image distance from the second principal point.
        ɑ= Distance of the first principal point from first lens.
        β= Distance of the second principal point from second lens.

From figure, ( using sign convention)
           
        -U = -u +ɑ
         U = u - ɑ
And. V= v -β

 For lens combination

  1 _ 1 = 1    and magnification m = V
  V   U    f                                               U

     
               

Cardinal points of an optical system

Cardinal points of an optical system:

               A  combination  of  lenses  having common  principal axis is  called a coaxial system of lens. In such  systems, a  method for finding out the distance and size of  the image is very tedious. Gauss showed that a coaxial system  can  be  considered  as  one system. For any system of lenses, there are six points known as cardinal points.

  They are:

  i) two focal points F₁ and F₂
  ii) two principal points P₁ and P₂
  III) two nodal points N₁ and N₂.

             Consider a coaxial optical system of two convex lenses of focal lengths f₁ and f₂ placed at a  distance ‘a' apart  as  shown  in figure.

Focal points :

 
             To explain the first focal point on the object  side  refer  figure. A.  Consider  an incident ray of light AB passing through axial point F₁. After refraction through lens system this ray becomes parallel to the principal axis ( in a direction CD ). Then this axial point F₁ through which rays are incident on the lens system is known as first focal point. A plane passing through F₁ and perpendicular to the principal axis is known as first focal plane.

Focal point

              To explain second focal point on image side refer figure.B. consider incident rays parallel to the principal axis. After refraction through the lense system, these rays focus on the axial point F₂, then this axial point F₂ is known as second focal point. A plane passing through F₂ and perpendicular to the principal axis is known as second focal plane.

Principal points:

                 In  figure .A.  incident  ray  AB produced forward and emergent ray CD produced backward to meet at E. A vertical plane passing through this point E and perpendicular to the principal axis is known as first principal plane. The point where the first principal plane intersect the axis is known as first principal point. Here P₁ is the first principal point. The distance P₁F₁ between first principal point and first focal point is known as the first principal focal length of the system.

                In  figure  B.  Incident  ray  GH produced forward and emergent ray KJ produced backward to meet at M. A vertical plane passing through this point M and perpendicular to the principal axis is known as second principal plane. The point P₂ where the second principal plane intersect the is known as principal point.

                 Principal  points  are  the  points having unit positive magnification for lens system. The distance between first focal point and the first principal point is known as first principal focal length ( P₁F₁ ) of lens system. Similarly the distance between second focal point and second principal point is known as a second principal focal length ( P₂F₂ ) of lens system.

Nodal points : 

                 Nodal points are the two conjugate points on the axis of lens such that the relative angular magnification is unity. When the light ray is incident at an angle  Rita , on the first nodal point N₁, emerges from the optical system at the same angle Rita from the another nodal point N₂. It means these are the points on the axis having unit positive angular magnification. So, the nodal points have a property that the rays , through these points are parallel to each other. The plane which passes through nodal points and perpendicular to the axis XX' are known as nodal planes.

                When the medium on both sides of optical system in same, then the nodal points and principal points coincide.

Gravitational potential due to a uniform solid sphere

Gravitational potential due to a uniform solid sphere:

1) At a point outside the sphere:

                    Consider a uniform solid sphere having radius  R and  mass  M.  Let  P  be  a point at a distance ‘r' from the centre Of the solid sphere, where the gravitational potential due to the sphere is to be determined.

                      Imagine the solid sphere to be made  up  of  a  large  number  of  thin  concentric spherical shell's of masses m₁, m₂, m₃, ..... etc. Now, the gravitational potential at P due to whole sphere is equal to sum of potentials due to all such shells.

                 .•. V = - [ Gm₁+ Gm+ .....]
                                   r            r

                         = - G ( m₁+ m₂ + .....)
                               r

                 .•. V = - GM
                                r

Where, m₁+m₂ + .... = M = Mass of the sphere.

Intensity  of gravitational field due to solid sphere:

E = - dV   =   - d  ( - GM )
         dr            r        r

.•. E = - GM
               r²

                     Negative sign shows that, the intensity of gravitational field is directed towards the centre O of the sphere.

2) At a point on the surface of the sphere:

At a point on the surface of the sphere, r=R :

V = - GM    and
           R
E = - GM
           R²

3) At a point inside the sphere :

           Consider a uniform point P inside the sphere at a distance‘r' from its centre O , as shown in figure.

Let R = radius of sphere  and
 ϱ = density of the sphere

           Now, with O as a centre and radius OP = r drawn a sphere.

           Then the point P lies on the surface of the solid sphere of the radius ‘r,' and inside the spherical shell of internal radius R and external radius R.

.•. volume of inner solid sphere = 4 π r³
                                                                 3

.•. Mass of inner solid sphere = 4 π r³ϱ
                                                            3

The potential V₁ at P due to inner solid sphere is :

V₁ = - G ( 4πr³ ϱ )  = 4πr² ϱ G     ..... (1)
                     r

               To find the potential V₂ due to the outer spherical shell, draw two concetric spheres of radii ‘x' and ( x + dx ) ,  forming a thin spherical shell of thickness ‘ dx '.

              .•.  Volume of shell = 4πx² dx

              .•. Mass of shell = 4πdx²dx

              .• Potential at P due to this shell

              P  = - G (4πdx²dx )   =   -4πdGx dx
                                  x
              .•. The potential V₂  at P due to thick spherical shell is obtained by integrating above equation between the limits x=r to x=R.

                 V₂ =  -4πϱG ᷊∫  ᷢᷢᷢᷢᷢᷢᷢᷢx dx = -4πϱG [x²/2] ᷊ ᷢᷢᷢᷢᷢᷢᷢᷢ

             .•. V₂ =  -4πϱG [ R² - r²]
                                              2

             .•. V₂ = -2πϱG ( R²-r² )    ......(2)

             .•. Total potential at P is given by :

                  V = V₁+V₂

             .•. V = - 4 π r²ϱ G-2πϱ G(R²-r²)
                          3

             .•. V = - 2πϱ G(2 r² + R² - r²)
                                      3

            .•. V = 2πϱ G(3R²-r²)
                       3

            .•. V =  -G( 4  π R³ϱ ) [3R²-r²/2R³]
                               3

                V = - GM [ 3R³- r²] .......(3) ,
                                      2R³
                Since,  4 πR³ϱ  = M
                             3

           This is an expression for the potential inside a solid sphere, at a distance, from its centre.

            The minimum potential at the centre of the sphere can be obtained by putting r=0.

             V₀= -3GM   ......(4)
                         2R

             The intensity of gravitational field at P inside the solid sphere is:

            E = - dV  =  -  d [-GM ( 3R²-r²)]
                     dr         dr               2R³

            E  = - GM [2r]
                      2R³

       .•. E = - GM   ... .... (5)
                     R³

Gravitational potential due to a spherical shell

Gravitational potential due to a spherical shell:

1) At a point outside the shell:

Consider a uniform spherical shell of radius R.

Let P be a point outside the spherical shell at a distance ‘r ' from the centre O of the shell.

Let ϱ = Mass per unit area of the surface.

As shown in figure, two planes AD and BC cut the shell vertically.

The element between the two planes is a slice ABCD in the form of a ring  of small angular width dϴ with the OP as axis.

Each element of the ring is at a distance , AP = x from the outside point P.

.•. Thickness of the shell, AB = R dϴ 

Radius of the shell, CK = R sinϴ

.•. Surface area of the slice= (2πR sinϴ) (R dϴ )  = 2πR² sinϴ dϴ 

.•. Mass of the slice= Surface area of  slice× Mass per unit area (ϱ)

Figure: Gravitational potential at a point outside the spherical shell.

.•. Mass of the slice, Mring = 2πR²sinϴ dϴ ϱ

.•. potential at P due to the ring is :

dV = - GMring
                X

      =   - G(2πR²ϱsinϴ dϴ )/x    .....(1)

      In ∆ APO :    x² = r² + R² - 2rR cosϴ

Differentiating above equation, we get :

      2x dx = 2rR sinϴ dϴ      
                           ( since,R and r are constant ) 

      .•. x = rR sinϴ dϴ 
                     dx

Substituting this value of ‘x' in eq. (1) , we get :

dV = - G ( 2πR²ϱsinϴ dϴ ) dx 
                     rR sinϴ dϴ

     

     = - 2πRϱG dx

              r

Integrating above equation for the whole shell between the limits, 

x = ( r- R ) to x = ( r+R ) , we get :

But, 4πR²ϱ = M   ( Mass of the whole shell )

.•.  V = - GM 
                 r     ...... (2)

Thus, for a point outside the shell, the shell behabes as if the whole mass is concentrated at the centre of the shell.

Now, the intensity of gravitational field at a point outside the shell is given by:

E = - dV / dr  

  

   = - d / dr ( - GM / r )

.•. E = - GM / r²      ...... (3)

Negative sign shows that intensity of gravitational field is directed towards the centre O of the shell.

(2) Potential on the surface of the shell :

For a point on the surface of the shell, r= R.

.•. Potential ,  V = - GM / R

Intensity of the field,  E = - GM / R²

Guass’s theorem for gravitation

Guass’s theorem for gravitation:

              Guass's law states that the total  gravitational  flux  over  a closed  surface,  having  a  unique outward  drawn normal to  it  at every point is - 4πG times the  total mass enclosed by that surface.

                The gravitational field E at a distance ‘r' from a point mass M is given by :

                 E= - GM/r²    .....(1)

                 Then the flux (ϕ) of the gravitational field, through the surface of the sphere of radius ‘r' is given by :

                  ϕ = - GM × 4πr² = - 4πGM

                            r²   

                  As shown in  figure, this flux  ϕ  is  due  to  the  normal component of gravitational field 

                 E = - GM cosϴ

                           r²

                  Let , dϕ = small flux through an  element  of  area  dA.

               .•.dϕ = -GM cosϴ dA  

                              r²

               .•. dϕ= E.dA = n. E dA

               .•. Total gravitational flux enclosed by the closed surface is :

           ϕ = ∫ E. dA = ∫ n^. E dA

       .•. ϕ =  ∫ E1.dA +  ∫ E2.dA + ........

       .•. ϕ = -4πG (M1 + M2 + ......)

       .•. ϕ = -4πGM 

       where , M = sum of all masses enclosed by the surface.

This is Gauss's law in gravitation.

                          

Gravitational potential energy

Gravitational potential energy:

               The  amount  of  work  done  in moving  a unit  mass  from  infinity  to  the point  under  consideration ,  in  the gravitational  field  of  the  body  is  called gravitational  potential  at  that  point.

               The  gravitational  potential  is scalar quantity and it's S.I unit is joule/kg.

Gravitational potential due to a point mass :

               Consider a point A at a distance ‘r' from a particle of mass M, as shown in figure.

               Then intensity of Gravitational field at point A is given by:

                E = - GM/r²   (along AM )

               .•.   Difference   of   Gravitational potential between two points A and B at a distance ‘dr' apart is :

                VA-VB= dV = - E dr     .......(1)

                .•. E = - dV/dr                ....... (2)

                This  is  the  relation  between gravitational  field  and  gravitational potential.

                 .•. the gravitational field is defined as  the  negative  gradient  of  gravitational potential.

                  Now, from eq. (1) , we get:

                  dV = - ( - GM/r²) dr = GM/r² dr

                  Hence, potential V at point A ( i.e work  done  in  moving  unit  mass  from infinity to point A) in the gravitational field of M is given by:

                   Thus, gravitational potential is zero at infinity. And  at all other points it is less than zero i.e it has a negative value.

Gravitational potential energy:

                    The  gravitational  potential energy  of  a  body  at  a  point  in  the gravitational field is defined as the amount of work done in bringing the body from infinity to the desired point.

                    Consider a point A at a distance ‘r' from a  body  of  mass M.  A  particle  of mass ‘m' is placed at B , at a distance (r+dr ) in the gravitational field of M.

Gravitational force of attraction acting on mass ‘m' is :

                      F = - GMm/r²  (along AM )

                     Hence, the work done (dW) by the force F in moving the mass‘m' from B to A , through a small distance ‘dr' is given by:

                     dW = - F dr = - (- GM/r²) dr

.•.  total work done in moving the mass ‘m' from ∞ to point A is given by:

                  .•. W = - GMm/r      .....(1)

                  This work done is stored in the body as it's gravitational potential energy (U) and it is given by :

                   U = - GMm/ r       .......(2)

.•. Gravitational P.E (U) =gravitational potential (V) × mass of the body (m)

                   Gravitational potential energy (U) is always negative . It is a scalar quantity and it's SI unit is joule ( J ).

Gravitational field

Gravitational Field

               The gravitational field is the space around a body within which any other mass experience a gravitational force of attraction.

Intensity of gravitational field at a point:

                It is defined as the gravitational force acting on a unit point mass, placed at a given point, in the gravitational field of the body.

                 Consider a body of mass M which sets up the gravitational field in the space surroundings it.→

                  Now, a small test mass ‘m' is placed at a point P at a distance ‘r' from the mass M. The test mass ‘m' experience an attractive gravitational force F.

                 Then the intensity of gravitational field E at point P is given by:  E=F/m

                 The intensity of gravitational field is a vector quantity.

      The direction of E is same as that of F.

                 The magnitude of gravitational field strength at point P is :

                 .•. E= F/m = - GM/r²      .....(1)    

                 since, F= - G Mm/ r²

                 Negative sign shows that the field is directed towards the mass M , In vector form, the intensity of gravitational field can be given as :

                 E= GM/r² r^  ....... (2) 

                 Where, r^= unit vector along the line of force.

                  It's SI unit is N/kg and 

dimensions are [M°L¹T-²].